ジャパンネット銀行住宅ローン初回返済額の計算方法

住宅関連

2020.08.23

ジャパンネット銀行の住宅ローンの初回返済額の計算方法が気になったので確認してみました。
なお、住信SBIネット銀行の住宅ローンの初回返済額も同じ計算方法のようです。

まず結論です。
初回の返済額は「2か月目以降の毎月の返済額」に「借入月分（借入日～毎月返済日）の日割りでの利息分を追加」した金額です。

例えば、
10/9に借入、11/27が初回の返済日だとすると、10/9~10/27までの分の利息^(*1)と10/28~11/27の通常の1ヶ月分の支払いの合計額になります。

(*1): 借入日も１日としてカウントするようで、この場合19日分の利息。

もう少し詳しく見ていきましょう。
金利（年利）: \(\alpha\)
月利: \( \beta = \alpha / 12 \)
日利: \( \gamma = \alpha / 365 \)
返済回数^(*2): \( N = 35 [年] \times 12 [ヶ月] = 420 [回]\)
とすると、

(*2): 35年ローンを想定。

毎月の返済額は \[毎月返済額= \frac{借入金額\times \beta \times (1+ \beta )^N}{(1+\beta)^N -1} \] です。ただし、小数点以下は切り捨てます。

そして借入月分の日割りでの利息は \[借入月分利息= 借入金額\times \gamma \times 日数 \] です。ただし、こちらも小数点以下は切り捨てます。

では実際に計算してみましょう。
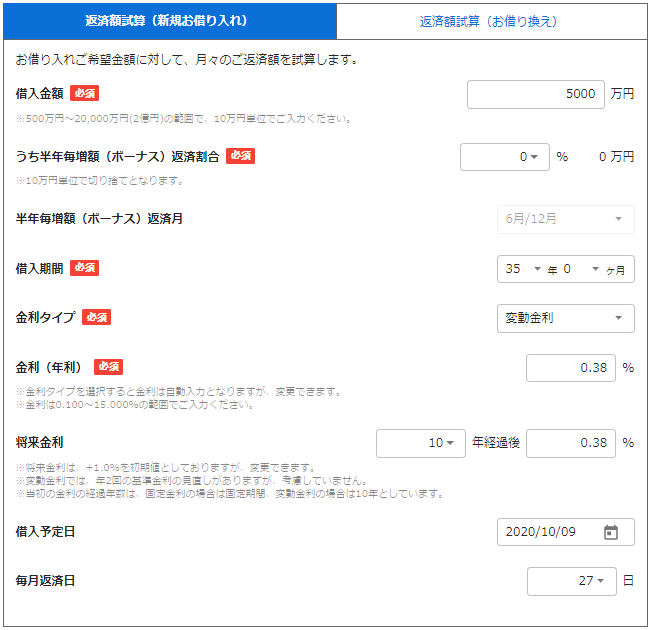
借入額を5,000万円、借入日10/9、毎月返済日27日（初回返済日11/27）、金利を2020年8月の変動金利の値0.38%（\(\alpha = 0.0038\)）とすると

毎月の返済額は \begin{align}毎月返済額&= \frac{50,000,000\times (0.0038/12) \times \{1+ (0.0038/12) \}^{420}}{\{1+(0.0038/12)\}^{420} -1} \\ &=127,158.5 \\ &\rightarrow 127,158円 \end{align} です。

そして借入月分の日割りでの利息は \begin{align}初月分利息&= 50,000,000\times (0.0038/365) \times 19 \\ &=9,890.4 \\ &\rightarrow 9890円 \end{align} 従って、初回支払額は\(127,158+9,890=137,048\)円となります。

ジャパンネット銀行公式HPの住宅ローンシミュレーションで同じ設定でシミュレートしてみると、上の計算と一致しています。